It's rocket science

Introduction

In August we have all have been inspired by the Chandrayaan-3 mission, where mankind has for the first time landed near the Moon South pole. Inspired by the landing images and videos, I decided to re-approach the topic of propulsion since my time at uni. In this post I will derive the rocket equation, trying to get familiar with variable mass systems. Then I will integrate the equation in time under as set of not so stringent hypothesis. To convince myself of the correctness of the integration, I will present a simulation, in the form of an interactive game, in Javascript, that can run in your browser. Finally I will present a strategy to beat the game, using the suicide burn manoeuver.

The rocket acceleration

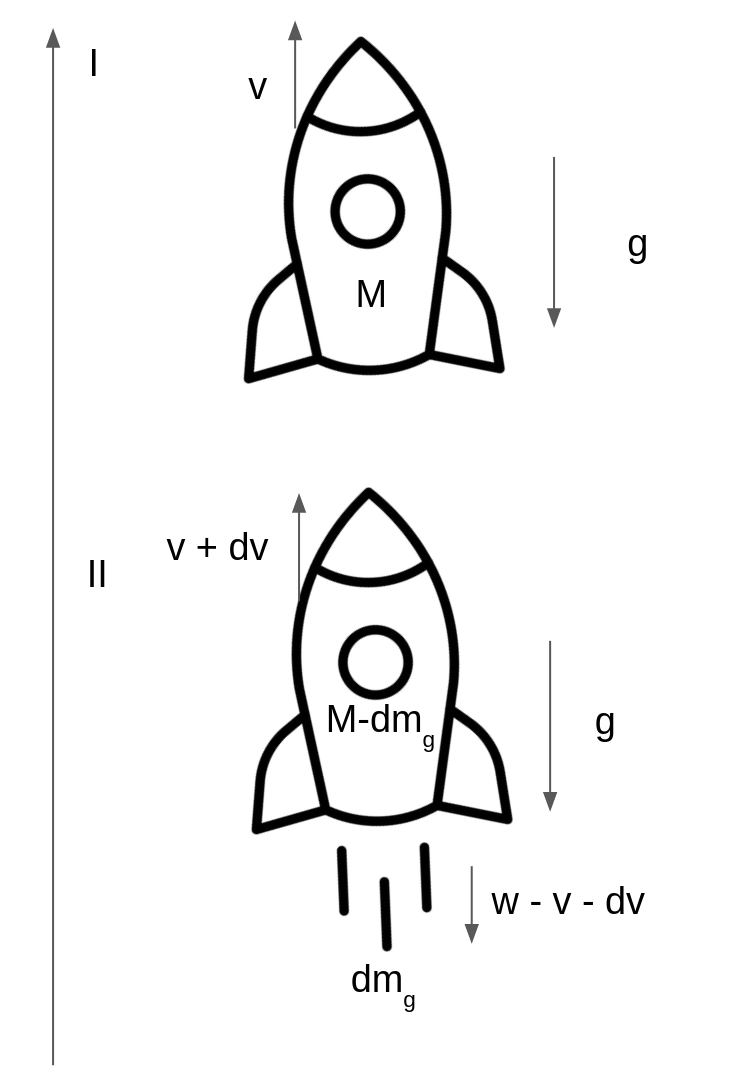To grasp the basics of the physics at play let’s start from a rocket, in a vacuum under the influence of gravity. Between instants I and II the rocket will experience a force from gravity pulling it downwards. At the same time, the rocket can contrast gravity burning some fuel, ejecting it with a velocity w. The ejection of mass will accelerate the rocket in the upwards direction. Since this is a varying mass system, the classical Newton’s second law cannot be applied. Therefore to write the equation of motion we will use the conservation of momentum $p$ between I and II. Note that $p$ is a scalar quantity under the assumption of thrusters and flight path aligned with gravity. Also, the conservation of momentum will be written in a fixed reference frame, where the total velocity of expelled gas is $v + dv - w$. Indicating as $p_{II}$ the momentum at II and $p_{I}$ the momentum at I:

\[p_{II} - p_{I} = Fdt\] \[p_{II} = (M - dm_g)(v + dv) - (w -v - dv) dm_g \approx Mv + M dv - w dm_g\]

The $\approx$ sign above is because I have dropped higher order terms like $dm_gdv$

\[p_{I} = Mv\] \[p_{II} - p_{I} = Mdv - w dm_g\]

An increase of expulsed gas mass is equal and opposite to a decrease of rocket’s mass

\(dm_g = -dM\) Substituting this expression in the change of momentum $p_{II} - p_{I}$:

\[M dv = Fdt - wdM\]

I can relate the change in mass of the rocket with the mass rate $\dot{m}$ as:

\[M dv = Fdt - w\dot{m}dt\]

Dividing by $dt$ and $M$ both sides:

\[a = \frac{F}{M} - w \frac{\dot{m}}{M}\]

Since $ F = -Mg$

\[a = -g - w \frac{\dot{m}}{M}\tag{1}\label{1}\]

Equation $\eqref{1}$ represents the instantaneous acceleration of a rocket with varying mass $M$ expelling gas at a rate of $\dot{m}$ under the influence of gravity. Since the mass is decreasing, $\dot{m} < 0$, and so the acceleration, as expected has two contrasting contributions: gravity and propulsion.

Integration of acceleration

In order to derive the position of the rocket over time, under the influence of gravity and thrusters, I will make 2 assumptions:

• The rocket burns fuel at a constant rate of $k$.
• The mass of the rocket decreases linearly over time depending on the fuel rate. i.e. \(M = M_0 - kt\tag{2}\label{2}\)

Where $M_0$ is the initial mass of the rocket and fuel onboard. Substituting $\eqref{2}$ into $\eqref{1}$

\[a = -g + w \frac{k}{M_0 - kt}\tag{3}\label{3}\]

Equation $\eqref{3}$ can be integrated in time to obtain the velocity

\[v = v_0 + w \log{\frac{M_0}{M_0 - kt}} - gt\tag{4}\label{4}\]

Equation $\eqref{4}$ can be integrated again in time to obtain the position

\[x = x_0 + v_0 t - \frac{1}{2}gt^2 + w \frac{M_0 - kt}{k} \log{\frac{M_0 - kt}{M_0}} + t\tag{5}\label{5}\]

Simulating rocket descent

Thanks to equations $\eqref{4}$ and $\eqref{5}$ given some data about the rocket such as mass and velocity of gas expulsion and gravity, I can now simulate the descent of the rocket, given a certain fuel rate. The assumption of constant fuel rate, it not so stringent because I can assume that for small increments of time the mass change in the rocket can be linearly approximated, and therefore the descent can be simulated using the equations derived. I have actually found a plethora of games on lunar descent that let you simulate this process, so I have decided to create my own replica of Lunar Lander in Javascript. The premise is that you lunar lander is falling towards the Moon and every 10 seconds you can decide to burn some fuel at certain rate. The objective of the game is to slow down the lander and land safely. You can give it a try here. You can read more about the original version of the game here. I tried different strategies to beat the game, with some success, but next I want to describe an algorithm to get a baseline for the fuel rate to input.

Computing fuel rate for the suicide burn

Suicide burn is a powered descent in which a constant fuel burn rate is applied until touching the surface, at a velocity of 0 m/s. In terms of the game it means finding the constant input to insert until the game ends. So how to compute this magical/mythical number? I did try to get an analytical answer, but opted for a more practical and pragmatic approach. The idea is as follows: if I burn all of the fuel at the maximum rate I could end up without fuel, too high from the surface and gravity will accelerate the rocket too fast to the ground. If I burn all the fuel at a very slow rate, I will end up with too much speed on the surface and crash land, as well. The solution I am looking for could be a fuel rate $k$ such that the fuel cut-off time is very close to the surface, and the velocity is not too high.

From the current altitude:

• For a given fuel rate compute the time at which the fuel will run out, know as burn time $t_b$
• Compute the position from equation $\eqref{5}$ given $t_b$
• If position is bigger than 0 (remember that 0 denotes the surface), decrease fuel rate, otherwise increase it.
• Once I find a suitable $k$ satisfying the above, decide to accept or reject solution if at $tb$ velocity is too high.

Using the algorithm above I was able to find a solution starting from the initial altitude of the game. The computed rate is 75.28 $\frac{lbs}{sec}$.

Conclusions

In this post I explored the math and physics of 1D rocket descent, inspired by the recent descent on the Moon of the Chandrayaan-3. I created a small Javascript replica of a Moon Lander game, and computed the suicide burn manoeuver. What I would like to explore for future posts are the following topics:

• Add a proper GUI interface to the game.
• Simulate at least the 2D motion.
• Add an Earth lander stage, including drag effect.
• Create an AI to find other solutions to the game.